I encountered these case studies while completing the Udacity course "Data Structures & Algorithms in Python". This seventh module doesn't contain any practice problems to enforce the information learned in their wonderfully developed videos, but I had trouble fully grasping the concepts in just a few minutes. If you are feeling similarly, here are some written explanations for each case study explained in my own words.
Shortest Path Problem
On the topic of traversing graphs, the shortest path algorithm aims to find the path with the smallest sum of weighted edge values or the path with the least amount of unweighted edges. The latter is easy to understand. A good analogy for undirected weighted graphs is where each node is a location of a city in which you are on a tour and each edge represents a flight ticket with a certain price value. Out of the many possibilities of getting from one location to another, the "shortest path" you are looking for is the path in which you spend the least amount money from flight tickets.
<Dijkstra's Algorithm> Now, the most famous solution for the shortest path problem goes nicely with my analogy since it is often called a "greedy" solution. Let's say we are trying to get from LA to PHL. We assign a placeholder value for each node, by building a queue, until we encounter that node with its corresponding flight ticket price. We choose to go in the direction of the lowest price and extract, or remove, that node from the queue. We parse through all of the nodes this way until we 1) reach and extract the final destination node or 2) all the nodes but the starting node have the placeholder value (which means there is no solution).
Knapsack Problem
This one's a bit more intuitive because you've probably encountered this problem in real life when packing your suitcase for a trip! Each item you want to bring has a certain weight and value associated with it. What's the optimal solution for creating a suitcase (or knapsack) with the highest value with a given weight limit?? Sounds a little too familiar, right?
There's of course a brute force method for this, with an egregious run time. So let's talk about the faster approach. We associate the index with the item's weight, and its value as the....value or integer.
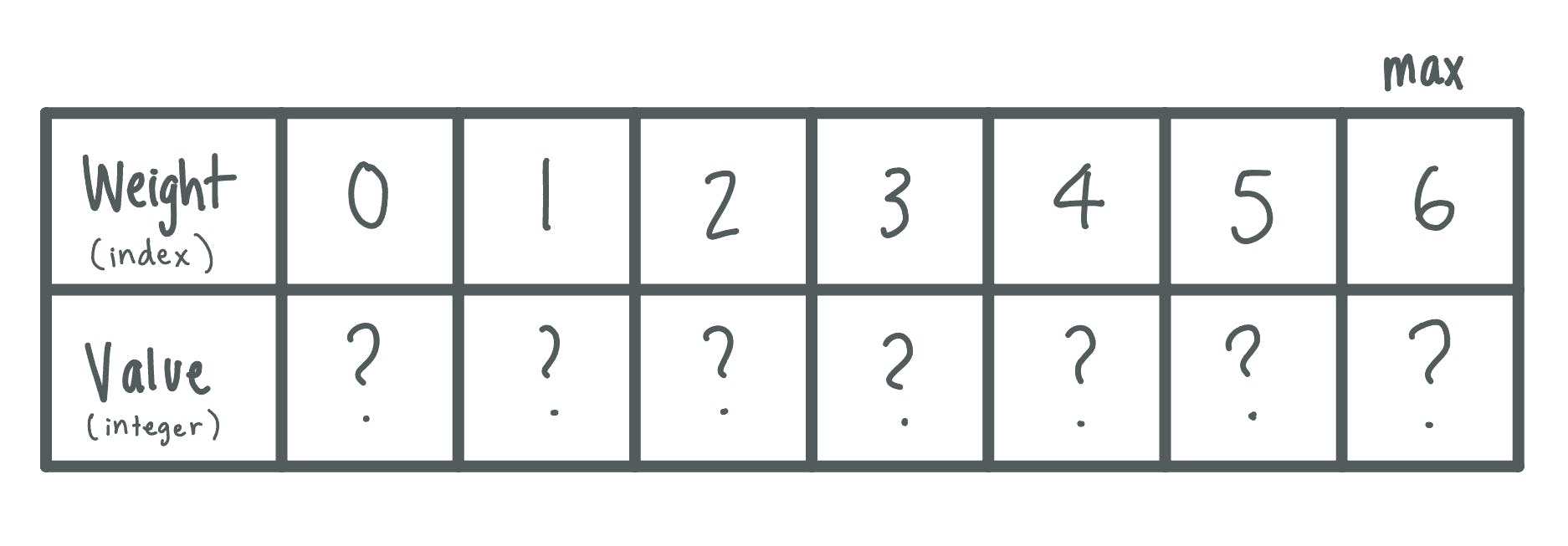Then, we can use recursion here to assess the value of each combination. W is the maximum weight the knapsack can hold. wt is the list of weights and val is the list of values of each object corresponding to that index. n is the length of items to evaluate.
def knapSack(W, wt, val, n):
K = [[0 for x in range(W + 1)] for x in range(n + 1)]
for i in range(n + 1):
for w in range(W + 1):
if i == 0 or w == 0: #if we have reached the zeroth index OR if the knapsack cannot hold anything
K[i][w] = 0
elif wt[i-1] <= w: #if the value we want to put in the knapsack is below the weight currently in that index, we replace it with the max
K[i][w] = max(val[i-1] + K[i-1][w-wt[i-1]], K[i-1][w])
else: #otherwise, we replace it with the higher value
K[i][w] = K[i-1][w]
return K[n][W] #we return the last item of the items in our table, which should be the max value of all the items
See a more in-depth explanation here
Traveling Salesman Problem
This is one of the first algorithmic-type problems I learned about! Revisiting it many years later (yes, it's been years since I've even thought about this type of programming), I'm reminded of why its an NP-hard problem. AKA...there is no known polynomial time solution! We won't go through the actual problem here, but there are many great resources, like this video, that explain why it is so complex.