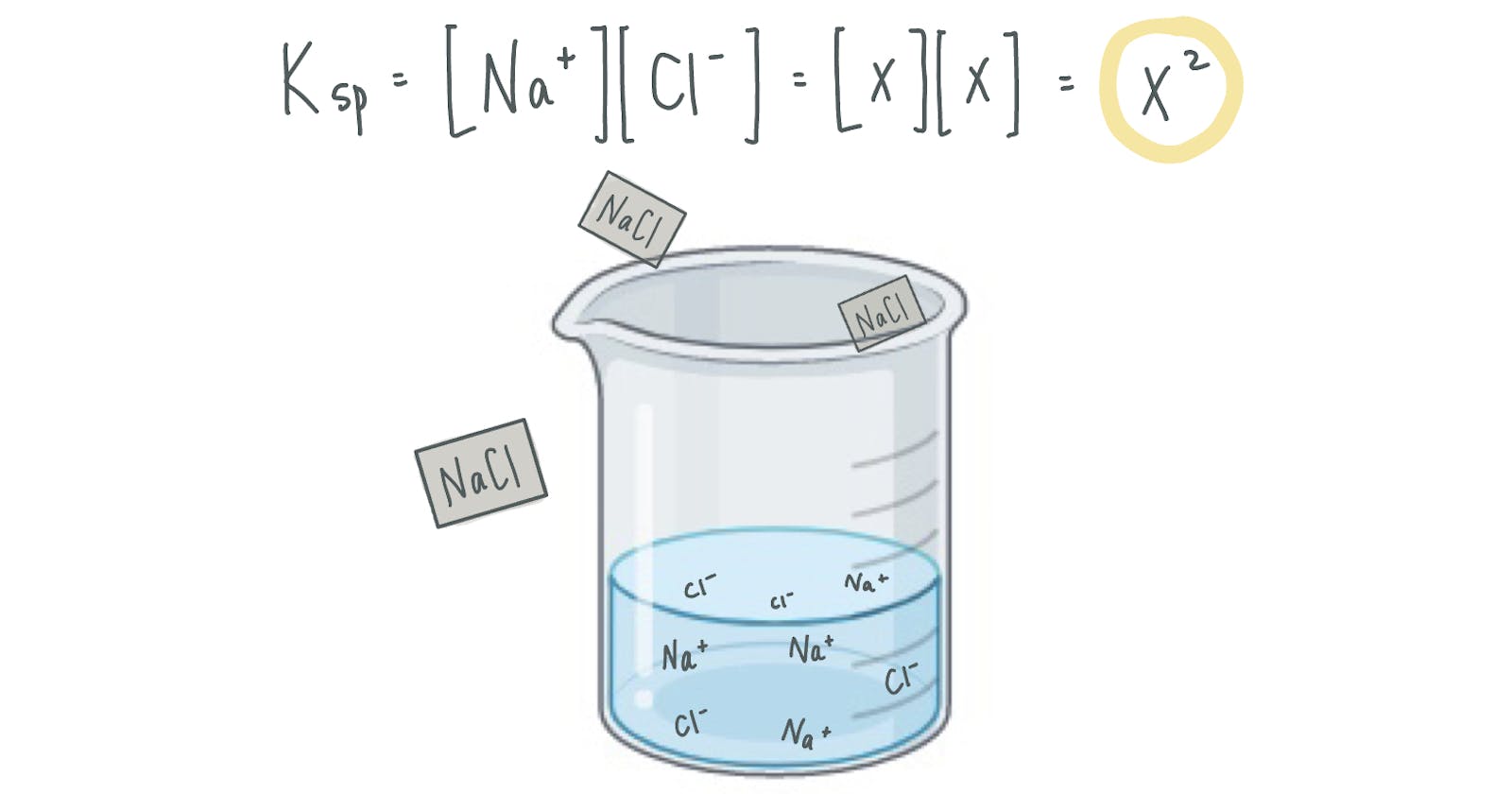Big O calculations can be tough to grasp as they feel wishy-washy in a sense. We end up memorizing the big O of common algorithms (and suggesting others to do the same), simply because it's easier. As I was going through and learning these big O notations, it struck me that the mathematics are incredibly similar to the concept of solubility. Depending on how many years ago your chemistry class was and how much your brain decided to block it out, conversion of Ksp to solubility may or may not ring a bell.
What happens when things dissolve?
Have you ever thought about why your garlic salt mixture doesn't dissolve in the oil they give you at Olive Garden? But we know that salt does dissolve in water. And pretty easily, right?
All compounds can be characterized as not soluble, slightly soluble, and soluble based on its Ksp constant. This value tells us how easily a substance can dissolve in water at a given temperature. The dissolution process actually results in a change in chemical composition, like below:
The NaCl molecule dissociates into its ionic components and the Ksp is expressed as:
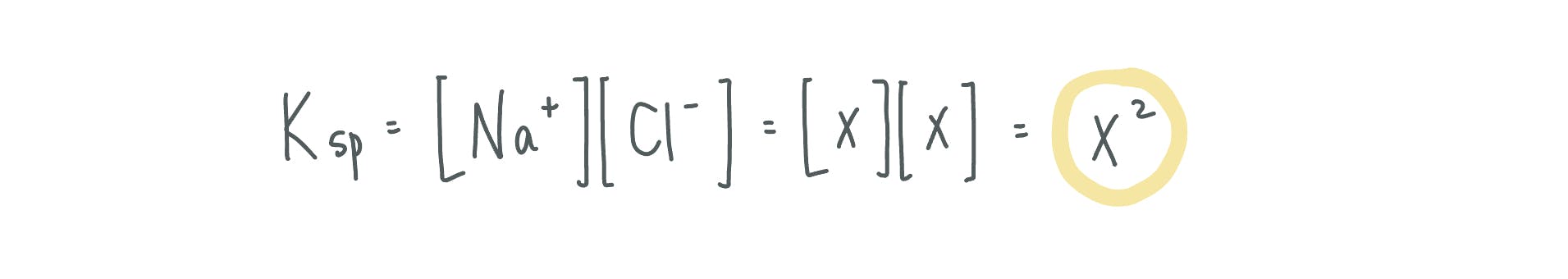
Calculation of Ksp
It might seem crazy to think that we could calculate the exact solubility value, but the calculation is very similar to that of big O. Let's say we have a cup of water that contains some other stuff in it like calcium chloride (0.1 M) and we want to dissolve some salt in it. Because of the chloride content already in the water, this will affect the solubility of NaCl relative to that in pure water. Now the calculation becomes:
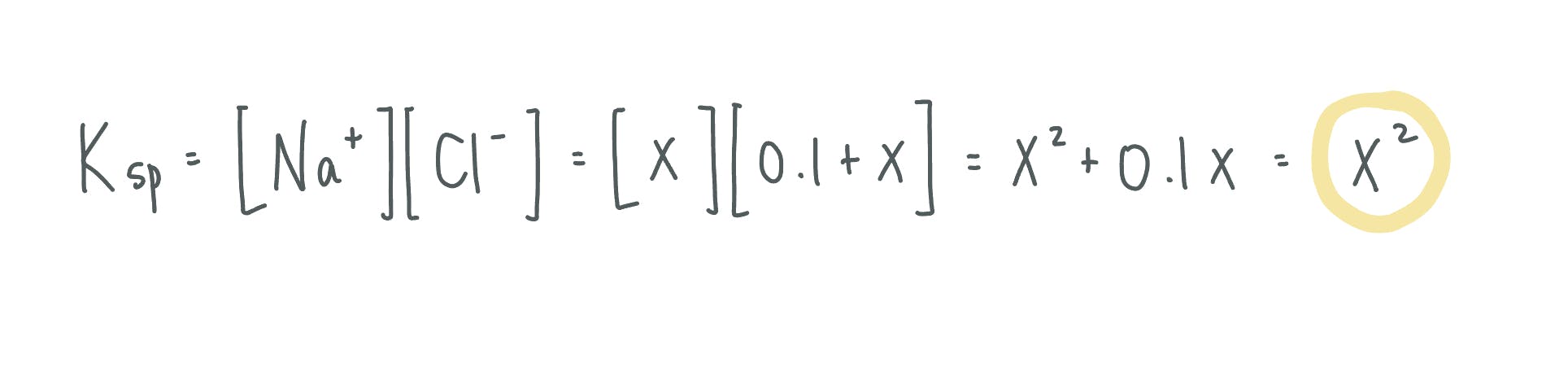But since the 0.1x term can be determined as insignificant compares to the x^2 term, we simplify this to x^2. Sound similar to big O calculations?
Big O simplifications
Let's take the example of the efficiency of binary search. Did you immediately think of the answer? Starting from the fundamental algorithm steps, we need to iterate 2^size of the array times. This can be written as O(log(n)+1), but the plus 1 term doesn't really change the efficiency very much. So this simplifies to O(log(n)).
Drawing relationships facilitate learning
If you are still following along, you may not feel as mind-blown as I was when I made this connection. Solubility and efficiency calculations are similar in the pattern of mathematical simplification rather than concept, but tying these two together has significantly helped me understand these concepts better. My hope is to share this interesting note and maybe help another:)